Calculando el Mínimo Común Múltiplo

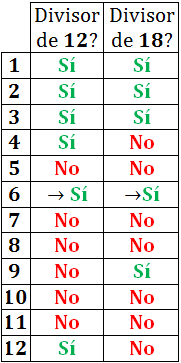
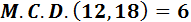El mínimo común múltiplo de dos números a y b es el número más pequeño que es múltiplo de a y múltiplo de b.

Para denotar el mínimo común múltiplo de a y b escribiremosm.c.m.(a, b) ó mcm(a, b).

Ejemplo: Vamos a calcular el mínimo común múltiplo de 4 y 6.

Para ello, escribiremos los primeros múltiplos de 4 y de 6.

Recordamos que los múltiplos se obtienen multiplicando.

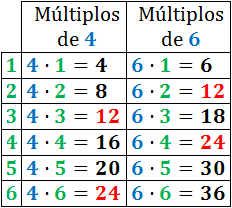
Entre los 6 primeros múltiplos de 4 y de 6 los números 12 y 24 son múltiplos de ambos (son múltiplos comunes).

Tenemos que quedarnos con el mínimo.

Por tanto, el mínimo común múltiplo de 4 y 6 es

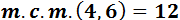
Fuente: https://www.matesfacil.com/ESO/numeros/minimo-comun-multiplo-definicion-ejemplos-ejercicios-test-problemas-descomposicion-primos.html

Calculando el Máximo Común Divisor

El máximo común divisor de dos números a y b es el número más grande que divide a a y divide a b. 

Para denotar el máximo común divisor de a y b escribiremos M.C.D. (a, b) ó M.C.D. (a, b).

Ejemplo: Vamos a calcular el máximo común divisor de 12 y 18.

Puesto que el número que buscamos tiene que dividir a 12 y a 18, no puede ser mayor que 12.

En la siguiente tabla escribimos los candidatos:

Puesto que el máximo común divisor debe dividir a los dos números, las únicas posibilidades son: 1, 2, 3 y 6.

Como tiene que ser el más grande posible, el M.C.D es 6.

Fuente: https://www.matesfacil.com/ESO/numeros/MCD/maximo-comun-divisor-MCD-definicion-ejemplos-ejercicios-resueltos-test-problemas-descomposicion-primos.html

Aplicacion de ecuaciones de primer grado en la vida diaria

Tenemos tres peceras y 56 peces. Los tamaños de las peceras son pequeño, mediano y grande, siendo la pequeña la mitad de la mediana y la grande el doble. Como no tenemos ninguna preferencia en cuanto al reparto de los peces, decidimos que en cada una de ellas haya una cantidad de peces proporcional al tamaño de cada pecera. ¿Cuántos peces pondremos en cada pecera?

Ver solución

x = número de peces en la pecera mediana

x/2 = número de peces en la pecera pequeña

2x =número de peces en la pecera grande

Como el total de peces es 56, tenemos la ecuación de primer grado

$$x+\frac{\mathrm{x/}}{2}+2x=56$$

Resolvemos:

$$3x+\frac{\mathrm{x/}}{2}=56$$

Tenemos que sumar las fracciones:

$$\frac{6x}{}+\frac{x}{}=56$$
$$2$$

$$\frac{7\mathrm{x\; /}}{2}=56$$

$$\mathrm{Procedemos\; a\; despejar\; la\; variable\; x}$$

$$\mathrm{(7x/2)\; *\; 2=(56)*(2)}$$
$$\mathrm{7x\; /\; 7=112/7}$$

$$x=16$$

Ya obtuvimos la cantidad de peces que se pueden colocar en la pecera mediana, como la capacidad de la pequeña y la grande es proporcional a la mediana,sustituimos dicho valor en la expresión algebraica de la pequeña y en la correspondientes a la grande, así determinamos la cantidad de peces que deben colocarse en cada pecera:

Peces en la pequeña x/2: 16/2=8
Peces en la mediana x: 16
Peces en la grande 2x: 2·16=32


Fuentes:
https://www.matesfacil.com/ESO/Ecuaciones/resueltos-problemas-ecuaciones.html